Introduction to Optical Coatings
In simple terms, an optical coating is one or more thin layers of material that affect how light interacts with a certain optical component. In order to understand how optical coatings work, it is important to know how light interacts with transparent media.
The index of refraction (n) of a medium describes how light behaves when travelling within it, with vacuum having an index equal to 1 and all other media having an index greater than 1. The reflection coefficient (R) of an interface between two media when the light hits perpendicular to the surface depends on their refractive indices:
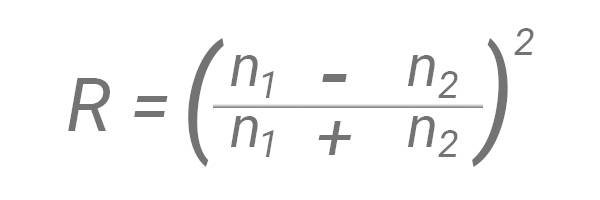
Where n1 is the refractive index of the first medium and n2 is the index of the second medium. The transmission coefficient (T) is defined as
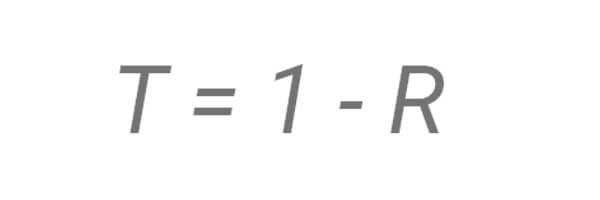
In the case of a light wave going from air (with a refractive index close enough to 1 to be rounded down) to glass (n ≈ 1.5) the reflection coefficient is 0.04 and the transmission coefficient is 0.96, which means that 4% of light is reflected and 96% is transmitted.
The properties of light that explain much of its behaviour when interacting with optical coatings can be explained by the wave theory of light. In this theory, light is described as a sine wave with a frequency (v) that determines the energy of the wave – the smaller the frequency, the higher the energy. In a vacuum, a light wave travels with a speed of c (approximately equal to 3 x 108 m/s) and the wavelength (λ) of the wave is related to its speed and frequency by the following equation:
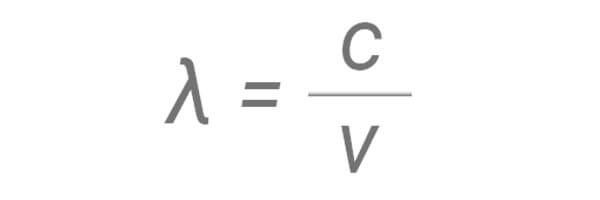
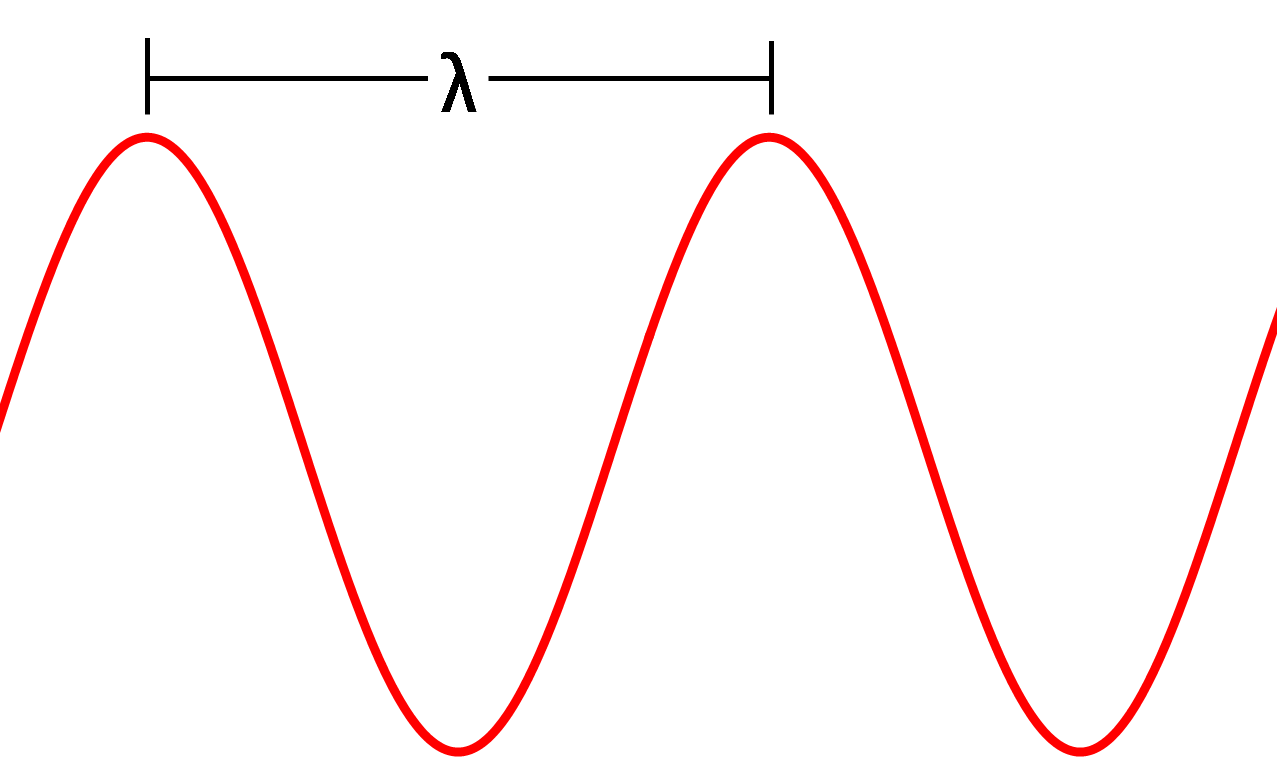
The wavelength is defined as the distance between two equal points in a repeating wave, such as the distance between the two peaks as illustrated in the figure below.
When a light wave travels through a medium, its frequency remains the same but the speed at which it travels in the medium (c’) is related to the speed of light in vacuum by the following equation:
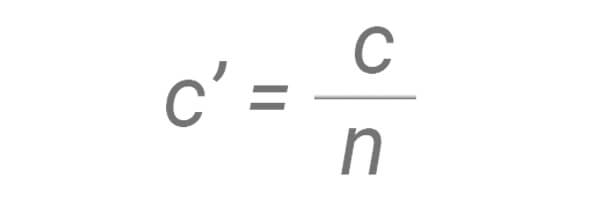
As such, the wavelength of the wave in the medium (λ’) is:
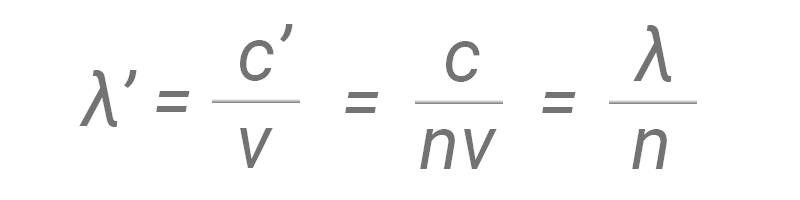
or
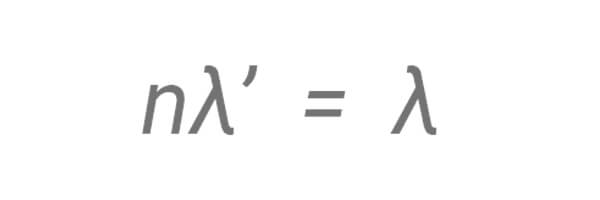
The optical thickness (OT) of a material is defined as the real thickness (d) multiplied by the refractive index, or
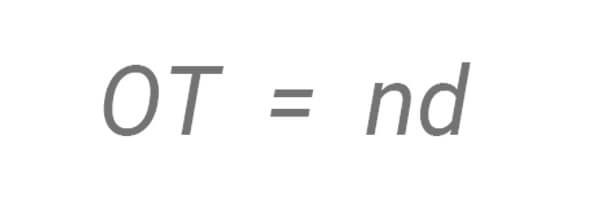
The optical thickness that light travels within a medium is thus equal to the real distance travelled by light in vacuum.
The wave nature of light allows for two or more light waves add their intensities together when they interact. If the phase difference between two light waves of the same wavelength is a multiple of a full wavelength (as shown in the figure bellow), the peak of one wave lines up with the peak of the other wave. The waves are said to be “in phase” and when this situation occurs, the intensity at each point doubles in a phenomenon called “constructive interference”.
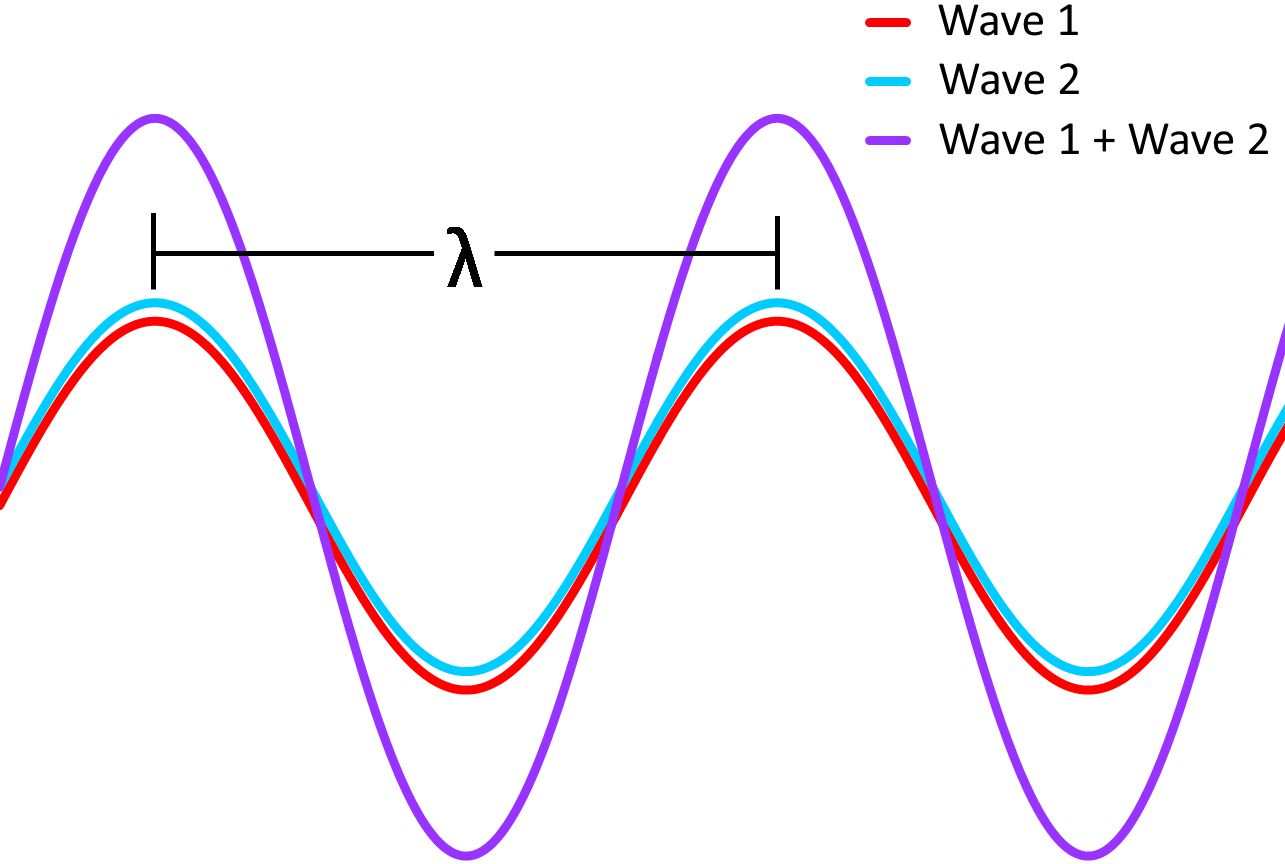
Constructive interference can be observed for other types of waves, not only with light. For example, rogue waves in the ocean are waves of water that are approximately twice as tall as surrounding waves. They occur when two waves meet, adding their heights together and forming a big wave that forms quite suddenly. In the case of light, constructive interference increases the intensity of the color of the wavelength that undergoes constructive interference.
On the other hand, if the phase difference between the waves is half a wavelength, the peak of one wave lines up with the valley of the other wave, as shown in the figure below. The waves are then said to be “out of phase” and when this occurs, adding the intensities of the waves cancel each other out in a phenomenon called “destructive interference”.
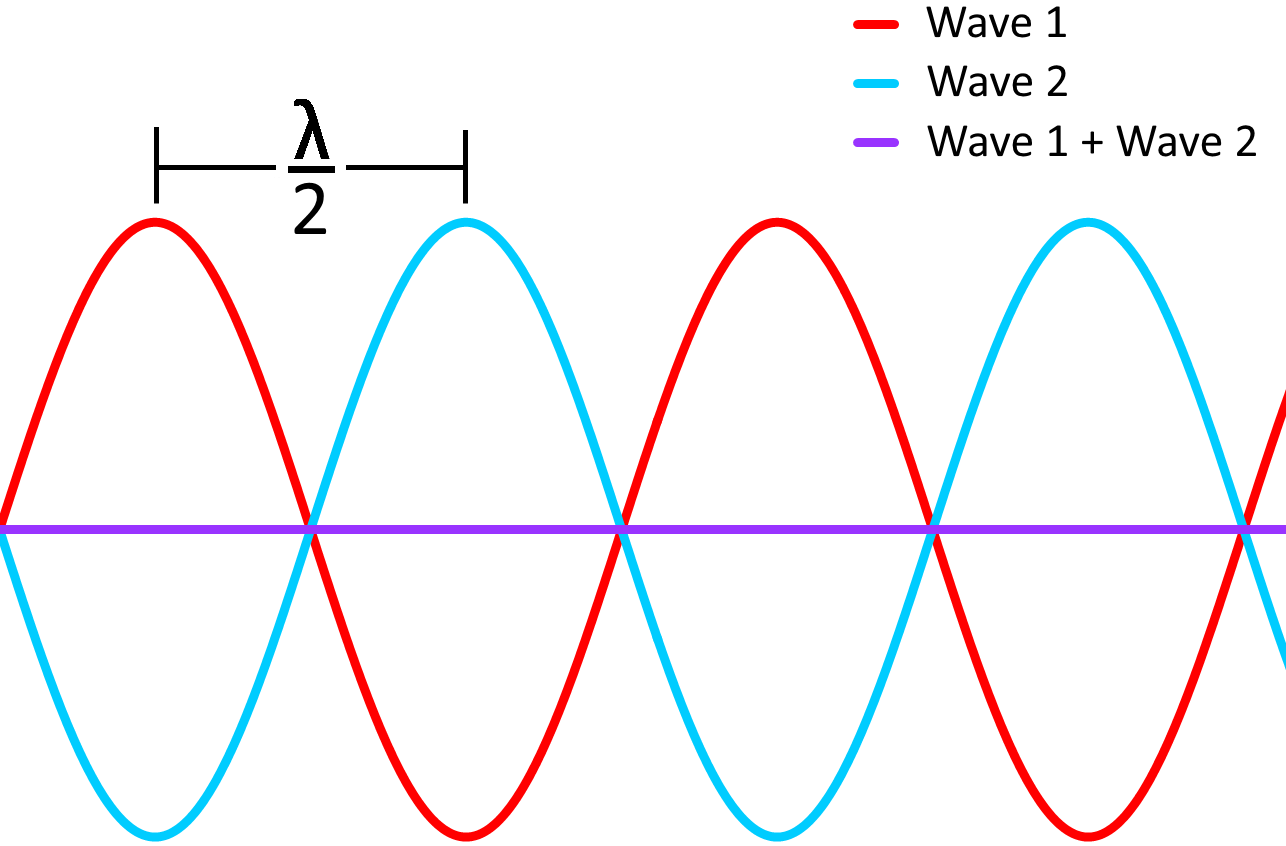
Destructive interference can happen with other types of waves, such as sound waves. For example, if in a concert there are two speakers in different places playing the same music, there are “dead spots” around the venue where the sound waves cancel each other. Noise-cancelling headphones use this same phenomenon to attenuate outside noise by outputting sound waves that match the frequencies of the noise but stagger them so that they cancel each other out.






